原文信息:
标题:Analyzing and forecasting volatility spillovers, asymmetries and hedging in major oil markets
作者:Chia-Lin Chang, Michael McAleer and Roengchai Tansuchat
单位:National Chung Hsing University, Erasmus University, Maejo University
原文刊发:Energy Economics 32(2010) 1445–1455
摘要:石油是能源中不可替代的部分,已经成为维系世界各国工业化经济正常运行的血液。石油价格波动也一直以来都是世界各国关注的热点问题。目前国际上四个主要的石油市场分别是北海布兰特原油(Brent)、西德州中级原油(WTI)、迪拜原油(Dubai)和马来西亚原油(Tapis)。本文通过三种多元GARCH模型(CCC模型、VARMA-GARCH模型和VARMA-AGARCH模型)实证检验了四个主要国际原油市场之间的溢出效应以及溢出效应的不对称性,并通过滚动窗口方法计算四个市场之间时变的溢出效应关系。实证结果表明大部分市场之间存在溢出效应,不同市场间时变的溢出效应则是上涨与下降趋势同时存在。最后,为了更好地针对原油市场进行风险管理,本文探讨了不同原油市场之间最优套期保值比例和最优投资组合投资权重的问题。
一、引言
近二三十年来,石油已经成为世界上最大的商品交易品种。原油市场上,石油一般通过合同安排、即期市场和期货市场进行交易。国际上石油交易的四个主要基准价格包括:1)西德州中级原油(WTI),美国石油的基准价格;2)北海布兰特原油(Brent),欧洲石油的基准价格;3)迪拜原油(Dubai),中东与远东地区的基准价格;4)马来西亚原油(Tapis),亚太地区的基准价格。
金融范畴中波动性或风险的概念十分重要,但波动性一般不可直接观测。现有研究表明金融市场的波动溢出效应普遍存在。波动性溢出效应以及溢出效应的不对称性对投资者构建最优套期保值比例和最优投资组合具有重要的指导意义。如何准确构建测度波动性的模型至关重要。资产价格波动性特征一般包括波动时变性、波动持续性、波动聚集性以及正负冲击的不对称性等。资产价格冲击中的可预测部分可以通过时变条件方差模型来刻画,比如VARMA-GARCH模型、VARMA-AGARCH模型、GJR模型等。
现货、远期和期货石油市场交易基础不同、流动性也不同,进而波动性特征也不同。本文则是探讨不同市场石油价格的溢出效应。在四个主要的国际原油市场中,只有最知名的石油市场,即WTI和Brent,有现货、远期和期货价格,而迪拜和马来西亚市场则只有现货和远期价格。因此,本文的主要目标是探讨同一市场内现货、远期和期货原油价格以及不同市场间三种价格的波动溢出效应,并在此基础上给出估计最优套期保值比例和最优投资组合的方法。
二、计量模型
本节主要介绍了固定条件相关系数模型(constant conditional correlation model)、VARMA-GARCH模型和VARMA-AGARCH模型。这些模型与维度无关,并且具有恒定的统计特征。
VARMA-GARCH模型假设资产价格服从ARMA模型,且正负冲击对条件方差具有等值影响,具体公式如下所示。其中,矩阵A衡量的是条件方差中的ARCH效应,矩阵B则衡量的是条件方差中的GARCH效应。不同石油价格的波动溢出效应即通过条件方差方程反映。
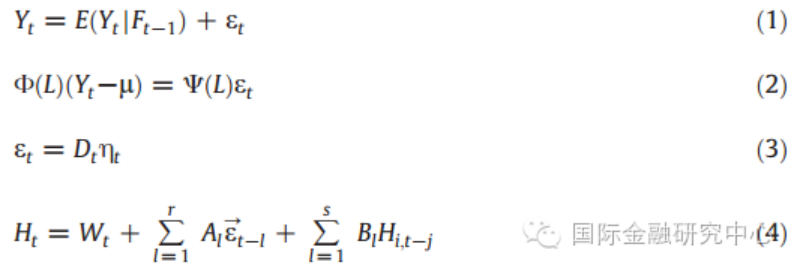
当考虑正负冲击的不对称影响时,我们可以考虑VARMA-AGARCH模型,即在条件方差方程中加入了表示负冲击的虚拟变量因子I。具体条件方差方程如方程(6)所示。
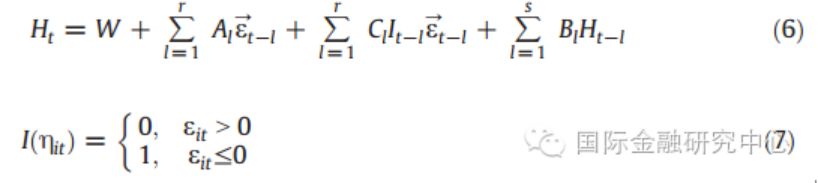
当矩阵C系数为零,且矩阵A和矩阵B为对角矩阵是,模型则简化为CCC模型。从定义可知,CCC模型中没有考虑不同资产之间的波动溢出效应,同时也忽略了正负冲击之间可能存在的不对称效应。CCC模型的条件方差方程具体如下所示。
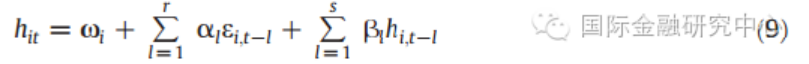
本文中采用最大似然估计方法上述均值方差模型中的参数。此外,我们用滚动窗口回归的方法预测一日后不同资产之间的条件相关性并且检验条件相关系数的时变性。综合考虑估计有效性和滚动回归可行数后,本文所有数据集选择的滚动回归窗口时间截止到2008年。
数据
单变量和多元的GARCH模型采取了四个主要国际原油市场石油现货、远期和期货的日度价格数据。时间跨度为1997年4月30日至2008年10月10日,共计3009个观测值。所有价格均用美元表示,资产价格收益率取对数收益率。通过ADF检验和PP检验,所有石油收益率均平稳。j市场i资产收益率如下公式所示。
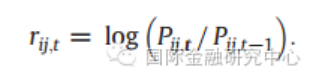
三、实证结果
本文首先通过单变量模型,即ARMA(1,1)-GARCH(1,1)和ARMA(1,1)-GJR(1,1)检验石油收益率的条件方差是否服从GARCH过程。结果表明,尽管部分均值方程系数不显著,但所有条件方差方程的系数均统计性显著。因此,GARCH模型是可行的。
由于迪拜原油市场和马来西亚原油市场缺少期货数据,本文共研究了10列收益率数据。为探究它们两两之间的关系,我们需要构建45个模型。
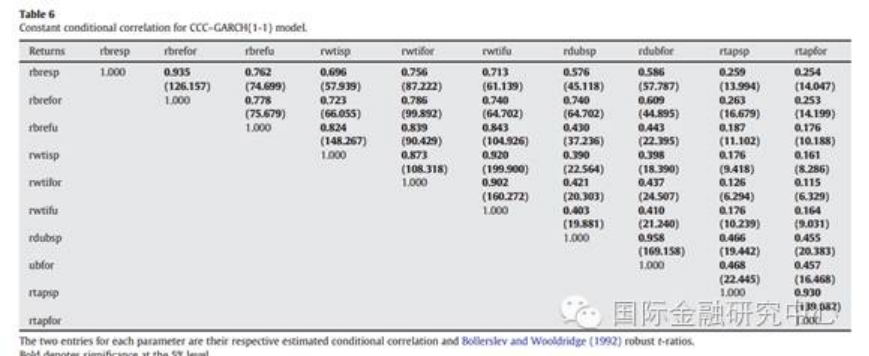
CCC模型的实证结果如下图(Table 6)所示。实证结果表明,Brent现货收益率和Brent期货收益率之间的条件相关性最强,系数为0.935。
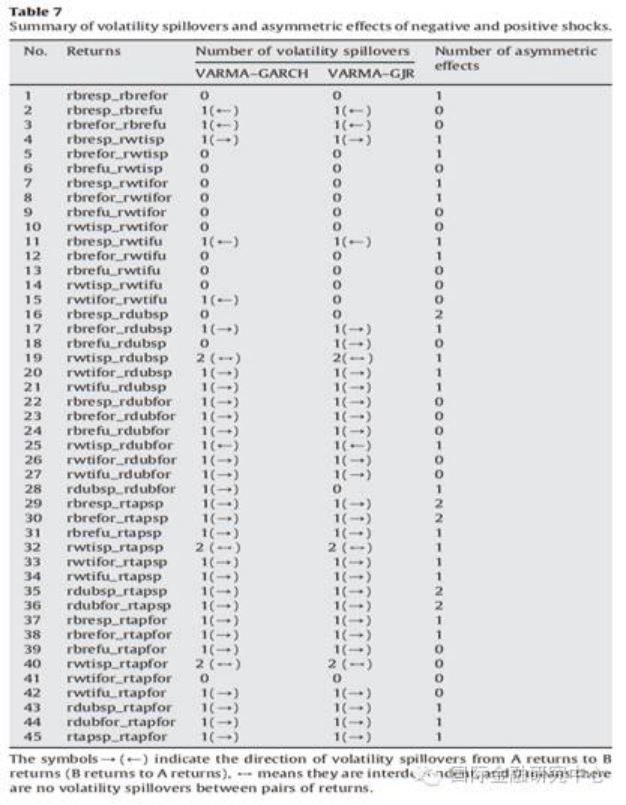
VARMA(1,1)-GARCH(1,1) 和VARMA(1,1)-AGARCH(1,1)模型的实证结果如下图(Table7)所示。实证结果表明,在所有的45种情况中,VARMA(1,1)-GARCH(1,1)模型有32种情况下具有显著的波动溢出效应,VARMA(1,1)-AGARCH(1,1)为31种。此外,两种模型下均存在3种具有显著双向波动溢出性的情况。45种情况中有27种情况不对称的波动溢出效应显著。考虑到存在波动溢出效应且正负冲击不对称,三种模型中VARMA-AGARCH为最优。
从VARMA-GARCH模型和VARMA-AGARCH模型的实证结果中可知,Brent和WTI原油市场价格之间存在双向的波动行溢出效应,比如Brent现货价格对WTI现货价格的溢出效应和WTI期货价格对Brent现货价格的溢出效应。与此相反,迪拜原油市场和马来西亚原油市场则是更多地接受来自Brent原油市场和WTI原油市场的溢出效应。考虑到Brent和WTI为国际上两个最为重要的原油市场,且其市场能决定原油价格并影响其他市场价格,本文的实证结果则间接证明了这一事实。
最后,本文通过滚动窗口估计VARMA-GARCH模型和VARMA-AGARCH模型参数的方法,得到不同市场间动态变动的条件相关系数。结果表明这些系数是时变的,并不恒定,进一步提供了CCC模型不可取的证据。此外,从系数变动的路径来看,有22种情况存在上升趋势,20种情况存在下降趋势。投资者在考虑构建分散化的投资组合时需要考虑到这种时变因素。
四、投资组合与套保策略设计
本节探讨投资于原油市场和其他市场的最优套期保值比例和最优投资组合权重问题。理论上,最常用的套保策略是基于最小组合方法原则,即最小方差套保比例。基于条件方差的动态最优套保比例如下所示。为了使风险最小化,每持有1单位原油资产多头,需要同时持有beta单位另一原油资产空头。

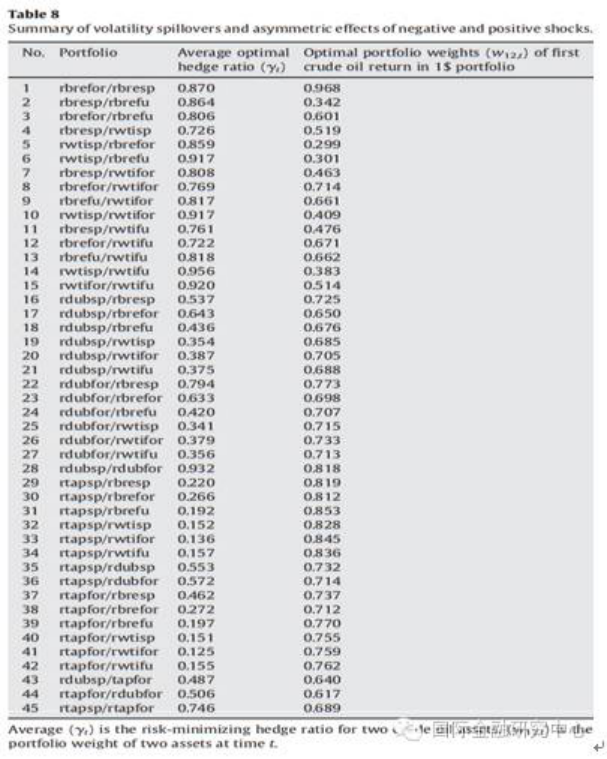
基于VARMA-GARCH模型的平均最优套保比例如下图(Table 8)第一列数据所示。最高的平均最优套保比例为0.956(rwtisp/rwtifu),即1单位WTI现货多头需要0.956单位WTI期货空头来对冲风险。此外,实证结果可知,Dubai和WTI、 Tapis和Brent以及Tapis和WTI之间的最优套保比例都相对较低。
最优投资组合即使组合方差最小的投资组合。本文通过VARMA-GARCH模型中估计的协方差矩阵来计算组合方差,并以此确定各资产在最优投资组合中的权重。资产1相对于资产2的权重可表示如下公式(12)所示。持有资产1权重为w,资产2的权重为1-w。

基于VARMA-GARCH模型的平均最优投资权重如下图(Table 8)第二列数据所示。从图中数据可知,相较于迪拜和马来西亚原油,投资者应该更多地投资于Brent原油和WTI原油。
五、结论
本文实证分析了四个主要国际石油市场(Brent、WTI、迪拜、马来西亚)现货、远期和期货收益率之间的波动溢出效应。时间跨度为1997年4月30日至2008年10月10日。本文采用的多元条件异方差模型有CCC模型、VARMA-GARCH模型和VARMA-AGARCH模型。VARMA-GARCH模型和VARMA-AGARCH模型实证结果表明溢出效应和不对称的溢出效应系数显著,进而证实VARMA-AGARCH模型较另两者要优。
本文结果指出Brent和WTI两个市场间存在相互的溢出效应,迪拜和马来西亚市场有来自Brent和WTI市场的单方向溢出效应。这一结果进一步证实了Brent和WTI这两个原油市场的国际地位。此外,本文还通过滚动窗口估计VARMA-GARCH模型和VARMA-AGARCH模型的方法,得到了不同收益率之间时变的条件相关性数据。结果证实不同石油收益率之间的条件相关性是时变的。构建具有最小方差的最优投资组合时,本文实证结果指出投资者应较大比例持有Brent和WTI市场产品。至于两个不同原油市场之间的最优套期保值比例问题,持有的来自Brent和WTI市场的长头寸仅需较小比例的迪拜、马来西亚市场产品空头寸即可实现套期保值。

